Back to library
About this topic: Fractions, decimals and percentages
Fractions, decimals and percentages can represent parts of a whole or parts of a collection.

Fractions
We can describe fractions in different ways using numerals, pictures and number lines. Here are some examples of how the fraction one half can be shown:
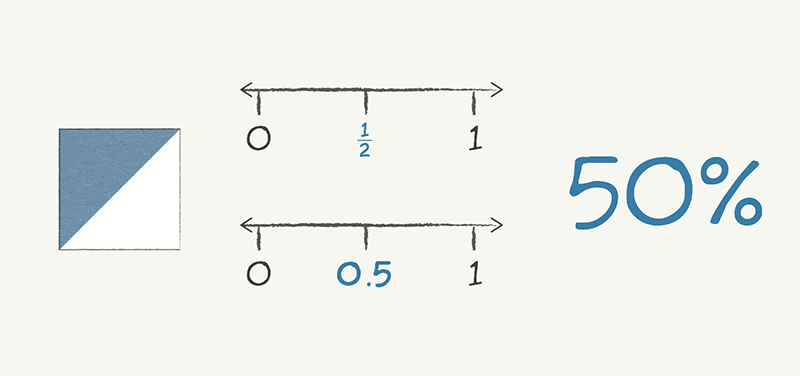
Looking at fractions
Fractions are made up of three parts:
- The numerator (the top number) tells us how many parts we have.
- The line separating the numerals is a way of showing division.
- The denominator (the bottom number) tells us the number of equal parts that the whole has been divided into. So the fraction 1/2 can also be written as 1÷2.

In schools children may learn the following types of fractions.
- Proper fractions, where the numerator (top number) is smaller than the denominator (bottom number), for example 2/3. Two parts of three equal parts.
- Unit fractions, where the numerator (top number) is 1. For example, 1/8 – one part of eight equal parts.
- Improper fractions, where the numerator (top number) is larger than the denominator (bottom number). For example, 5/4.
- Mixed numbers, which show us a whole number and part of a whole. For example, 1 1/4 shows us that we have a whole and a quarter (or five quarters, 5/4).
Decimals
Decimals describe fractional amounts using a number system based on tens. Decimals are a common way of describing fractions using place value (place value means that the value of a digit depends on its place in a number).
Decimals are especially useful when we need to be really precise about a small amount. For example, a biologist studying birds may take a precise measurement of the weight of its feathers.
Percentages
Percentages provide another common way of describing fractions using 100 as the denominator.
In our daily lives percentages are commonly used for:
-
statistics (94% of parents and carers in Australia believe play is important for their child’s wellbeing)
-
comparing relative quantities between groups where the actual number in the groups is different (28% of people in the USA drive white cars compared to 32% of Australians who drive white cars)
-
discounts (25% off recommended retail price)
-
increases or decreases over time (for example, the number of electric vehicles sold has increased by 60% since last year).
In all of these examples, 100% represents the total (either population or full price) even though the actual number of each thing is different.
Understanding fractions, decimals and percentages
There are a few key ideas that help us understand and work with fractions, decimals and percentages. These include:
-
partitioning
-
equivalence
-
benchmarking.
Partitioning
Just like whole numbers, fractions, decimals and percentages can be broken up or partitioned in different ways and still show the same total amount.
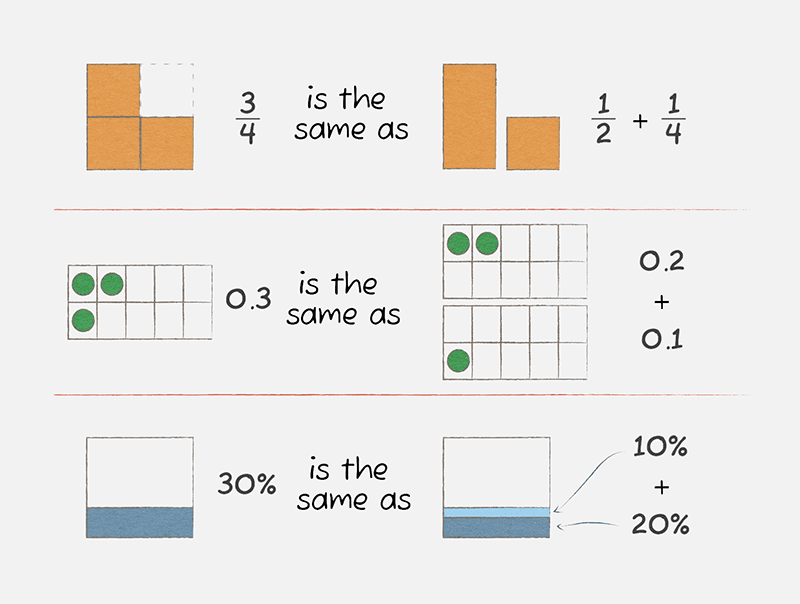
Partitioning fractions and decimals can make them easier to work with. For example, if we want to work out what 3/4 + 3/4 is we may partition one of those amounts into 1/4 and 1/2. We could then add the 1/4 to the other 3/4 amount to make up a whole, which leaves 1/2. So 3/4 + 3/4 = 1 1/2.
Equivalence
Fractions or decimals are equivalent if they represent the same part of the whole or group. For example: 1/2 is equivalent to 2/4 and 3/6 and 4/8 and 5/10.
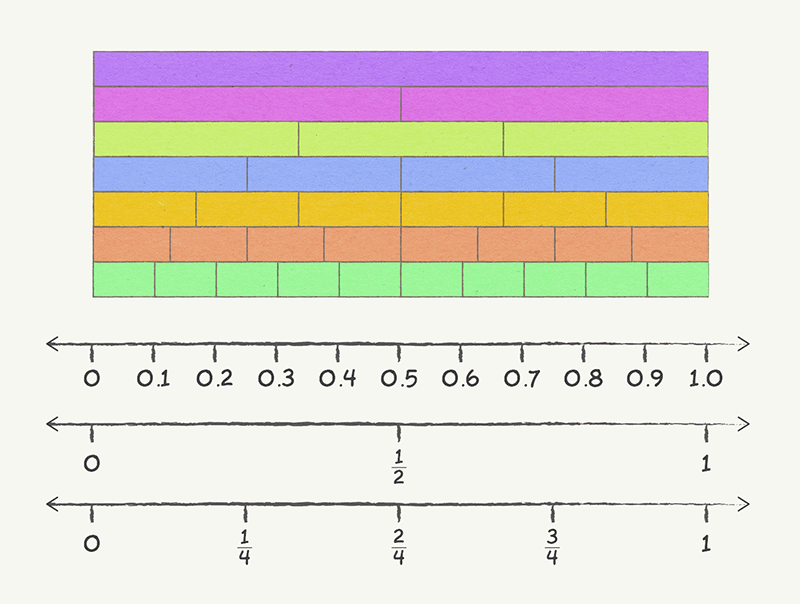
Remembering that fractions show us how many equal pieces a whole or group has been divided into and the number of pieces we are working with, we can see that 1/2 shows us the same amount of the whole as 2/4, 3/6, 4/8 or 5/10 it’s just that the size and number of pieces changes.
Fractions, decimals and percentages can also be equivalent to each other. For example, 1/2, 0.5 and 50% are all the same.
Understanding that the same amount can be said in different ways helps us solve problems that have mixed representations. For example, if something is on sale at 1/2 price and the shop offers an extra 25% off sale items, it is much easier to work out what the total discount is by adding 50% and 25% (or 1/2 and 1/4).
Benchmarking
Benchmarking is using a known quantity or number as a reference point when comparing, estimating or calculating. This helps us better understand the size of the fraction or decimal. For example, we might use 1/2 as a benchmark to understand that 3/4 is closer to 1 than to 0, or that 0.25 is closer to 0 than 1.
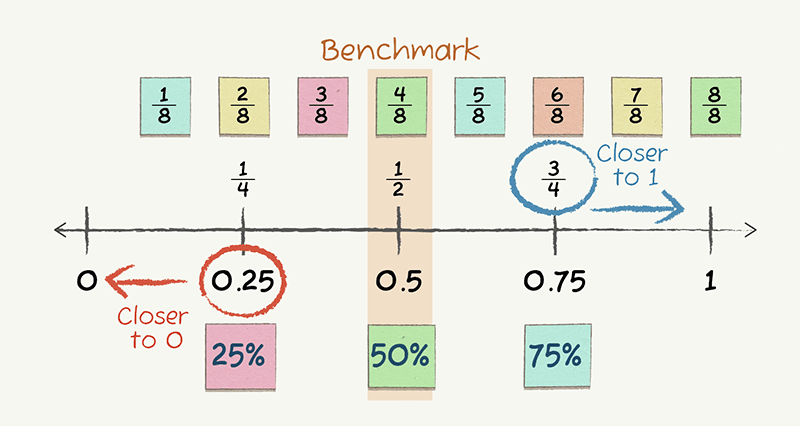
Possible misconceptions
Children usually learn about whole numbers before they learn fractions. Sometimes they apply the ideas used for whole numbers to fractions. Because whole numbers and fractions work differently, this can cause some misconceptions.
A few of the common misconceptions that children may have are:
-
adding numerators and denominators. This is where they think that they need to add the numerators together and also add the denominators together. For example, mistakenly adding 1/2 + 1/4 to get 2/6, instead of 3/4. This happens when the child sees those as whole numbers rather than remembering that the fraction is showing parts of the whole.
-
ordering by denominators or numerators. This is focusing just on the numerator (top number) or denominator (bottom number) when deciding which fraction is larger rather than looking at the fraction as a whole. For example mistakenly thinking that 1/9 is larger than 1/2 because when they are working with whole numbers 9 is larger than 2.
-
gap thinking. This is focusing on how many parts are needed to get the fraction to 1, instead of thinking about the size of the parts. For example, thinking that 4/5 and 7/8 are the same size because only part is needed in each case to make a whole, or that 2/3 is bigger than 6/8.
Some common misconceptions children may have with decimals:
-
the longer a decimal is, the larger it is. For example, children may think that 0.13657 is larger than 0.92, as they are applying whole number thinking and 13 657 is a larger whole number than 92.
-
the shorter the decimal is, the larger it is. For example, thinking that 0.4 is larger than 0.83. In this case they are using denominator thinking – the larger the denominator the smaller the part is.
-
the decimal point moves when multiplying or dividing by tens. Children need to understand that the decimal point does not move when multiplying or dividing, only the numbers change value.
