Back to library
How kids learn this at school: Addition and Subtraction
Addition and subtraction are really important skills, so teachers spend time building up children's skills using a few different approaches. This happens over several years.
Children are usually encouraged to work together with their classmates when developing these skills and understandings. They will be expected to talk to each other and explain their thinking to each other. They will learn from each other as well as from the teacher.
In general, your child will be encouraged to move through three stages during the learning process:
- Concrete: this means using real, physical objects like blocks.
- Visual Representation: using drawings or photos of real things.
- Abstract: using numbers to represent the physical objects.
Concrete
In the early years of school, your children will be given 'concrete' or real objects to practice with. They might use familiar items like pegs, blocks, teddies or cups.
For example, they may initially count out a group of six cups, then another group of eight cups. They will find the total by counting all the cups, then move onto counting on from one group to find the total.
For example: 6 cups, 7, 8, 9, 10, 11, 12, 13, 14.

As they move on to 2-, 3- and 4-digit numbers, they may make these numbers with such things as connecting blocks or popsticks, counting out ten sticks and bundling these together with a rubber band to make a 'ten'.
For example, when adding 19 and 32:
- they will bundle together 1 'ten' and lay out 9 single popsticks, to make 19.
- then they will bundle together 3 'tens' and lay out 2 single popsticks, to make 32.
- they will put them all together and add them up.

Visual representation
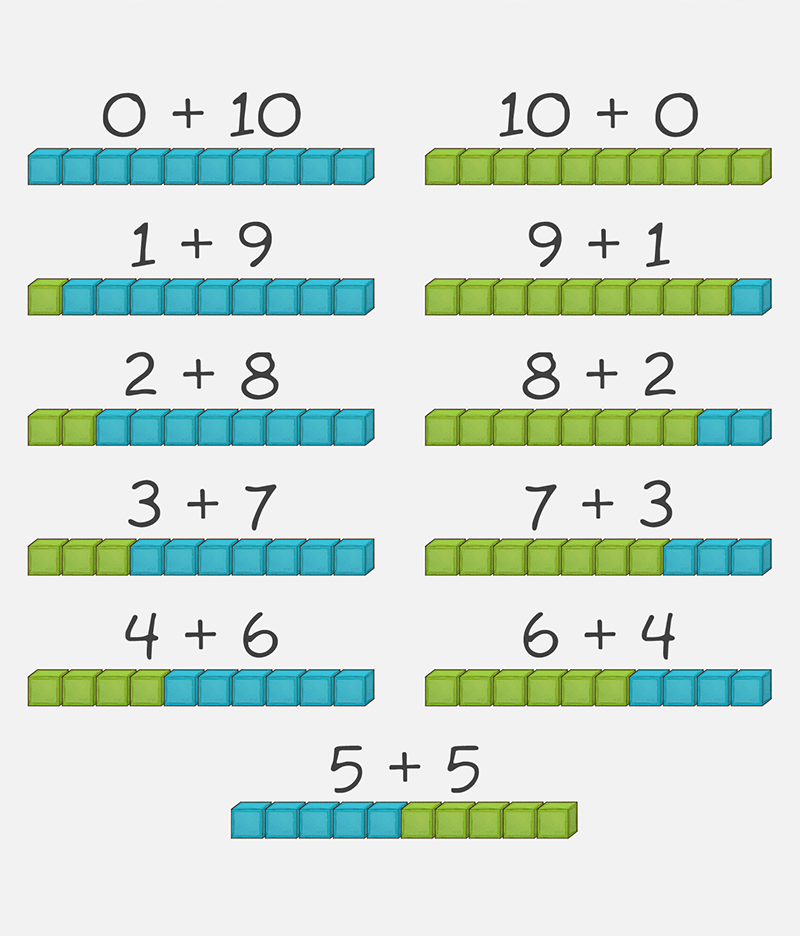
As they gain more confidence, your child will be asked to record what they did by drawing a picture of the teddies or popsticks or blocks. They will then be encouraged to represent this with symbols.
See below for example: 5 + 5 = 10, 9 + 1 = 10, and so on, represented as blue and green circles.
They will also be encouraged to 'take a picture' in their mind of the concrete materials and/or their drawings.

Abstract
Your child will be asked to imagine the physical objects, or their drawings (the picture in their mind), to help them solve addition and subtraction problems abstractly. This means solving problems without concrete or visual prompts.
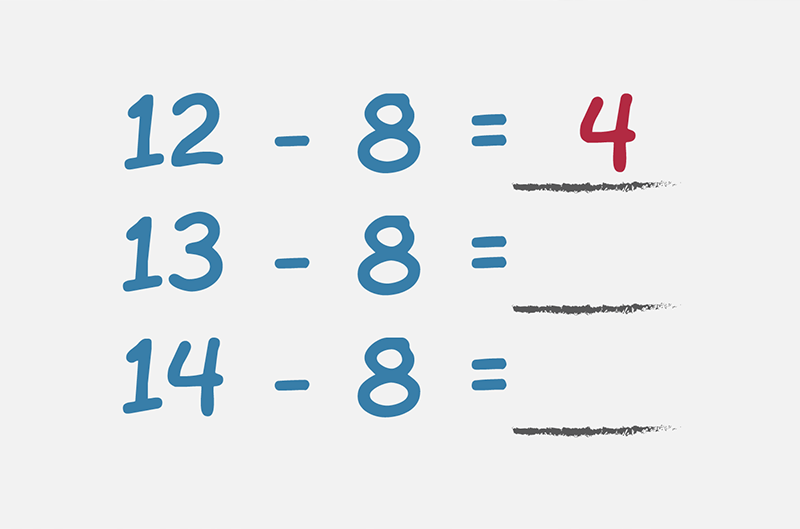
Basic number facts
Once your child understands the process of Addition and Subtraction, they will be encouraged to learn basic number facts. This involves the automatic recall of addition and subtraction facts up to 20, doubles and halves, number partners to ten and twenty (1 and 9, 2 and 8, 13 and 7, 14 and 6 etc).
The learning of these number facts is often experienced through a variety of card, dice, or board games. Automatically knowing these basic number facts will make it easier and assist your child with more complex addition and subtraction problems.
Maths learning strategies
Teachers use the word strategies to describe the different ways they help children understand things. There are several strategies that your child will be taught when solving addition and subtraction problems. They will learn that there is more than one way to solve the same problem.
Many of you will be familiar with the traditional 'long form' strategy for adding up or taking away numbers when you're doing maths problems. For example:
73
+ 14
_____
87
Teachers call this a vertical algorithm and, although these are still used, your child will be encouraged to try a few other strategies before they start using vertical algorithms.
Teachers will help children to automatically recall basic facts they have already learned, such as all the different numbers that add up to ten. Understanding how to partition (build up and take apart) numbers helps children get better at solving addition and subtraction problems. Multi-digit numbers can be built up or taken apart in a variety of ways to make them easier to work with.
These strategies are flexible, and teachers will encourage students to try various ideas, and will encourage them to come up with their own ways to successfully solve problems. This resource lists a few common strategies that teachers will encourage your child to use.
Possible strategies used during years 1-2 of school
Basic strategies
Your child will practice these strategies in the classroom, often through games. Once these facts are known automatically your child can use them to add and subtract larger numbers. For example:
Doubles: 23 + 23, double 20 is 40 and double 3 is 6, therefore 23 + 23 = 46
Adding Ten: 63 + 40, adding 4 'tens' to 63 is 73, 83, 93, 103, therefore 63 + 40 = 103
Tens Facts: 52 + 18, 8 + 2 = 10, so adding 2 'tens' to 50 is 60, 70, therefore 52 + 18 = 70
Derived strategies
When your child is fluent with using the above automatic basic facts, your child will be taught to use these flexibly and with some minor adjustments. For example:
Near Doubles: 7 + 8, using doubles for numbers close to being doubles, so 8 and 8 is 16 take away one is 15, therefore 7 + 8 = 15
Adding Nine: 74 + 9, adding 10 to 74 is 84, and then take 1 away is 83
Building to Nearest Ten: 36 + 7, to get to the next 'tens' you add 4 to 36 to get 40, then you add the 3 left over to get 43, therefore 36 + 7 = 43
Split strategies
This is where your child will use their ability to partition (break up/decompose) numbers to make larger numbers easier to work with. For example:
Breaking Up Numbers: 437 + 252 = ?
400 + 200 = 600
30 + 50 = 80
7 + 2 = 9
600 + 80 + 9 = 689, therefore 437 + 252 = 689
Possible strategies used during years 3-4 of school
Jump strategy
This strategy involves using a number line, starting with the first number in an equation and adding or subtracting by either jumping forwards or backwards in manageable jumps.
Using empty number lines to record these jumps are quite useful. For example:
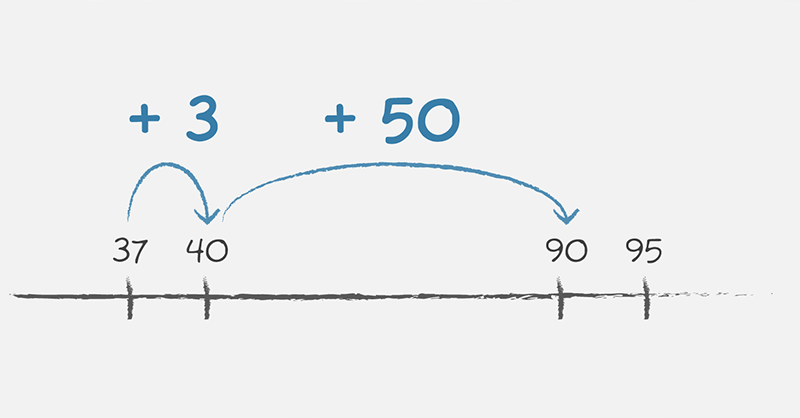
Using Jump Strategy: add these two numbers: 37 + 53 = ?
Starting with the first number of 37, you can jump 3 to the next nearest 'tens' and get to 40.
Then, jump 50 to get to 90.
Therefore 37 + 53 = 90
The jumps could also be completed by jumping by ‘tens’ first, 47, 57, 67, 77, 87, then jump 3 to arrive at 90. There may be other possibilities as well. These possibilities vary with the numbers that are used in the equations.
Empty number lines are a visual cue for your child. It also helps them to keep track of the jumps they have made to solve a problem.
Empty number lines can also be used for subtraction as well. Your child would start from the right and make their jumps below the number line. By distinguishing above for addition and below for subtraction it makes it possible to use both addition and subtraction to solve a problem if needed.
Compensation
This strategy involves changing numbers to make them easier to work with. If you add to one number, you need to balance this out by taking away an equal number from the other number. For example:
Using Compensation: add these two numbers: 99 + 24 = ?
Add 1 to 99 to make it 100, and take away 1 from 24 to make it 23. The equation now becomes:
100 + 23 = 123
Therefore 99 + 24 = 123
This strategy can make numbers easier to work with. It can also be completed on an empty number line as mentioned above. Solving this problem will involve both addition and subtraction, jumping above and below the number line.
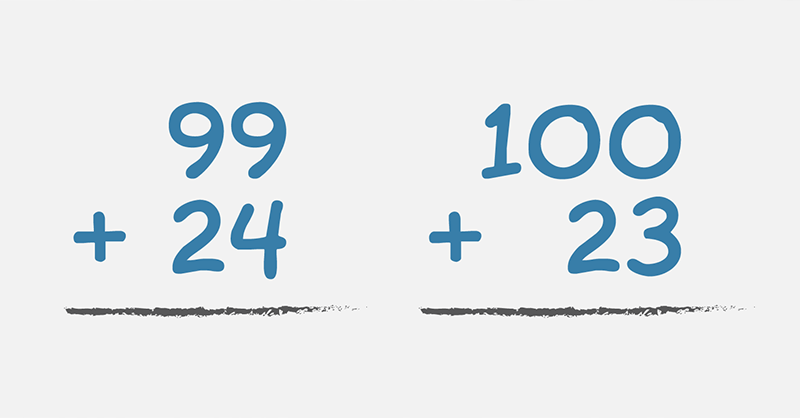
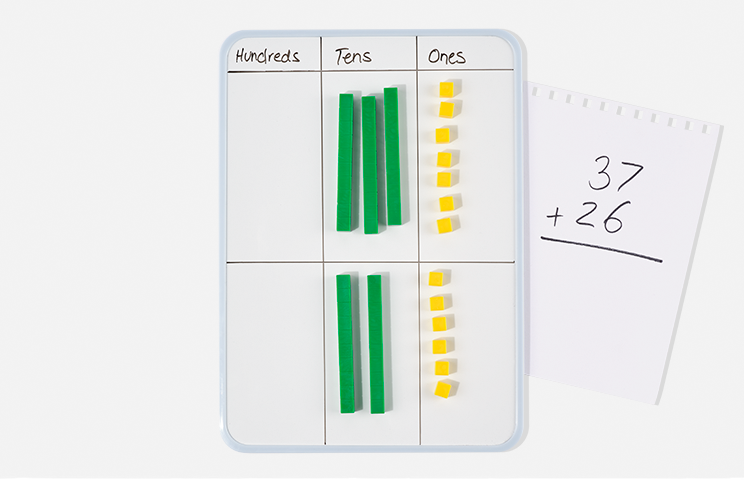
You might remember using such terms as 'borrowing' or 'carrying' when completing problems like the ones above. Your child will be discouraged from using such terms as they do not reflect the reality of what is really occurring. Terms such as trading, exchanging or renaming will be encouraged instead.
This is to help children understand that when you add 8 and 7 and you get 15 you are actually renaming 10 ones as one ten or exchanging the ten ones for one ten, when you put that '1' in the tens column to complete the problem.
Below is an example of how your child will be taught to understand the vertical algorithm. Connecting blocks or pop sticks, along with a Place Value mat will be used to concretely demonstrate how this algorithm works to allow your child a deeper understanding of what is happening during this process. They will physically trade or exchange the ten ones into one ten and place it in the tens column.
Because of the absence of concrete materials, using vertical algorithms to solve problems is very abstract and therefore taught last, after your child has a full understanding of what is occurring when using this method.
Possible strategies used during years 5-6 of school
All the above strategies will be introduced to your child by Year 4. In Years 5-6 and throughout subsequent years, these strategies will continually be reinforced and built upon. These strategies will gradually be used in more complex situations, such as with fractions and decimals.
Summary of strategies
As you can see from the above information, there are lots of different strategies that can help your child solve addition and subtraction problems. Teachers will emphasise that there is 'no one right way to solve addition and subtraction problems'.
Every child is different, so the strategies a teacher encourages your child to use will depend on what makes the most sense for your child in that situation.
As the famous mathematician George Polya once said, "It is better to work on one problem in many different ways, than to work on many problems in the same way".