Back to library
How kids learn this at school: Fractions, decimals and percentages
Fractions, decimals and percentages are topics some children find challenging to understand.
Fractions, decimals and percentages can represent parts of a whole or parts of a collection.
Teachers may invest time in developing conceptual knowledge, ensuring student understanding and reducing the opportunity for misconceptions to occur.

Children will usually learn fractions, decimals and percentages using a mix of concrete (physical) and visual representations to understand the concepts, before moving on to the abstract. This is similar to the way they learn whole numbers.
Fractions
Children will usually start learning common, simple fractions first, for example halves and quarters. They often work collaboratively with classmates because this allows them to learn from each other as well as the teacher, as they discuss the concepts and explain their thinking.
Concrete (physical) representations
Using concrete and visual representations helps children develop a clear understanding of fractions. Things that children can touch, move and rearrange (such as blocks, mats or paper) can really help them understand the concepts. Making sure that all the parts are equal is an important concept to understand. (There is no such thing as a ‘big half’!)
Teachers will often begin exploring the concept of ‘parts of a whole’ using blocks or flat shapes that are split into fractional parts. These help students to see the size of a range of different fractions and to manipulate them to form different fractions – pulling them apart or putting them together for smaller or bigger fractions – and understand that a fraction is relative to the size of the whole. These are called area models.
Because fractions can also represent part of a group of things, teachers will use collections of objects as another way to explore them. Any objects can be used to represent fractions of a collection or set, and teachers will often use counters, blocks or tiles.
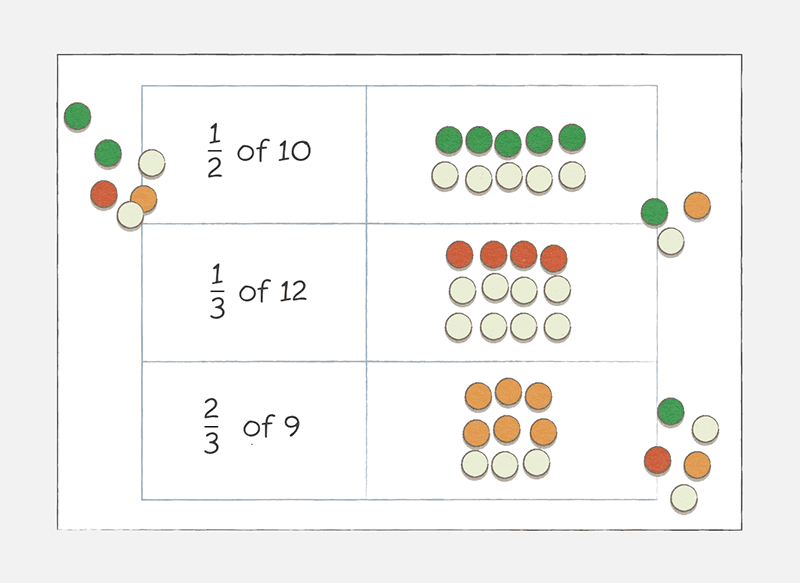
Visual representations
As children build their understanding of the relationship between parts and a whole or collection, teachers will introduce more visual representations. For example, teachers may use length models or bar models, which show fractions in regular-sized blocks.These tend to be easier for students to construct and use. The bar model can be used for the teaching of part-whole and for teaching fractions as a measure.
Abstract representations and problem solving
Once students have a sound understanding of the important ideas of fractions, teachers will reduce the reliance on physical or visual cues. They may introduce story problems that demonstrate different ways fractions are used in everyday life to deepen children’s understanding. Children will often be encouraged to use physical objects and or drawings when solving the problem.
For example, a teacher might present the following real-world problem:
Who gets more? Two people sharing 1 pizza or 3 people sharing 2 pizzas.
They may then encourage students to use their experience of physical and visual models to help them solve it.
Equivalences
When children have a good sense of fractions as a part of a whole, teachers will begin exploring equivalences.
This will usually start with equivalent fractions, then expand out to include decimals and percentages.
Equivalent fractions are fractions that are equal, even though they have different numerators (top number) and denominators (bottom number). For example, 1/2 is equivalent to 5/10 or 25/50.
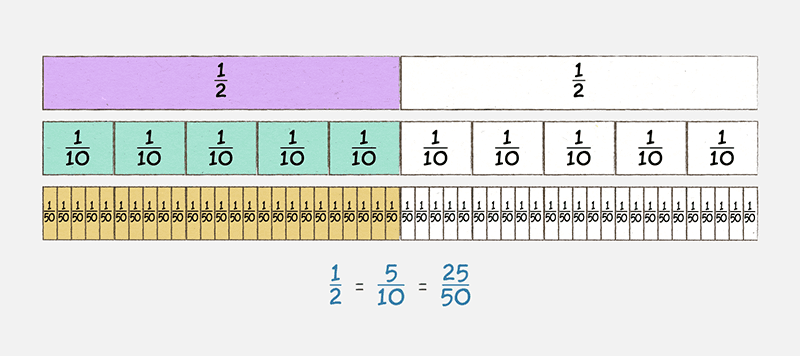
Understanding equivalences and being able to flexibly name fractions is important and teachers may spend a lot of time on it. It can be taught in many ways using a range of concrete and visual materials to build understanding.
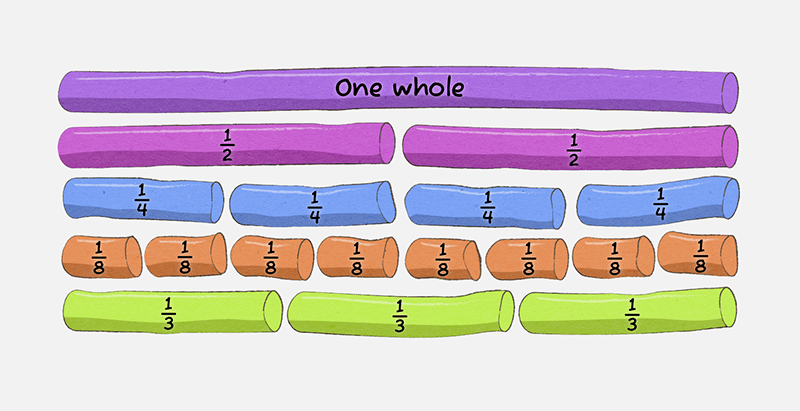
One way is through paper folding and creating a fraction wall. This is where students are given some equally-sized strips of paper to fold to help them see the size of equivalent fractions. Students label the first strip as 1 (whole). They fold the second piece into two equal parts (1/2) and label each part as 1/2. They continue adding more fractions until a wall is created. This helps them to see that fractions are equivalent if they are the same size. For example, 1/2 and 2/4 are the same size.
Fraction walls can also be made with blocks, playdough or plasticine.
As children become familiar with equivalent fractions, teachers will begin exploring other ways to show parts of a whole amount, such as decimals and percentages.
As with equivalent fractions, teachers may use a range of concrete or visual models to help children understand the relationship between a fraction and equivalent decimals and percentages. Many of the same physical and visual resources that are used to teach fractions (such as area models, sets and bar models) may also be used to teach these concepts.
Number lines are another useful way to show equivalent fractions, and their equivalence to decimals and percentages. They also show their size as part of a whole number.
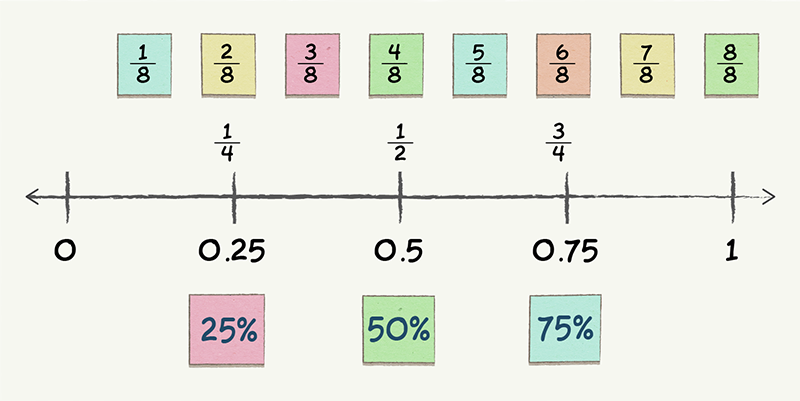
Ordering and benchmarking
As they are developing their understanding of fractions and their equivalents, children will also be taught ordering and benchmarking. These are key concepts that rely on an understanding of the size of fractions and how they relate to each other.
Teachers may ask children to order fractions and decimals from smallest to largest and then place them on a number line. This can be a complicated task and relies on a sound understanding of the size of fractions. Many children can be confused by the numerals used in fractions if they are using whole number thinking. For example, they may think 1/8 is bigger than 1/5 because 8 is a larger whole number than 5.
Visual representations can help children work through the concepts.
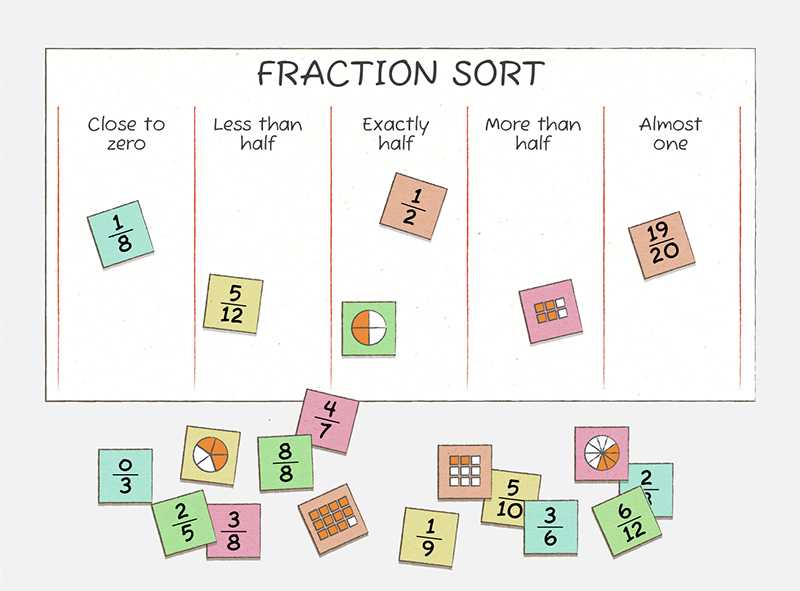
Likewise, children learn to use benchmarks. These are familiar quantities or numbers that they can use as reference points to help them estimate or quickly understand the size of a fraction, decimal or percentage. For example, they may use 1/2 (or 4/8) as a benchmark to estimate that 3/8 is closer to 0 than 1.
Teachers will give children activities that promote benchmarking. For example, they may be given a chart labelled with different benchmarks (such as close to zero, less than half, half, more than half and almost 1) and asked to sort a range of fractions, decimals or percentages by the closest benchmark. Children might use visual representations to help with this task.
Summary
Fractions, decimals and percentages can take a while for children to fully understand. Teachers use a range of physical and visual resources to help make the important concepts clearer and to support children as they build up their understanding of part numbers.
